Cube Torque Tester

When you read reviews of cubes you encounter lots of strange vocabulary that has been developed by cubers to describe concepts that don’t really exist outside of the cubing community.

Terms like buttery, crunchy, cripsy, blocky, bumpy, flimsy, and airy, (among others I’m sure!) describe the feeling of turning cube layers.

This is reminds me of the language that wine connoisseurs use to describe wine, where words describe sensations that don’t really make any sense except to people that have experienced those sensations many times.

But, I want to know if I can quantify these concepts. It seems like quantifying the sensation of turning a cube should be much easier than quantifying the flavor of wine.

My thinking is that if I can very precisely measure the amount of force required to turn a cube layer, then at least some of the descriptions of cube turning sensations should be identifiable in the resulting data. For example, a buttery turn should have a different looking force graph than a bumpy turn. I expect that I would be able to see greater friction in the bumpy turn, probably also greater variation in the friction as the cube turns. So, how do I test this?

My strategy is as follows:

1. Create a holder for a cube that allows the cube to freely rotate.

2. This holder will push on a load cell. (A load cell is a little electronic device that measures how much force is applied to it.)

3. After some amplification, the signal from the load cell is measured with an oscilloscope which essentially gives me a graph of force over time.

4. Then I just grab the top layer of the cube with my hand, give it a twist, and see what data I get!

So, I’ve done some initial tests with a crude cardboard model and a Qiyi Warrior, and it looks like this technique might actually be capable of producing interesting results!

In the video below, a cardboard cube holder is supported on an axle that can rotate. The corner the cardboard cube holder pushes on a load cell. When I rotate the top layer of the cube the friction between layers transmits some of this force to the cardboard holder and then to the load cell for measurement. The harder it is to rotate the cube, the greater the force on the load cell.

Below is a graph based on data saved from my oscilloscope. You can see the high initial torque required to overcome static friction, and then once the layer is turning the torque sharply drops to a lower torque.

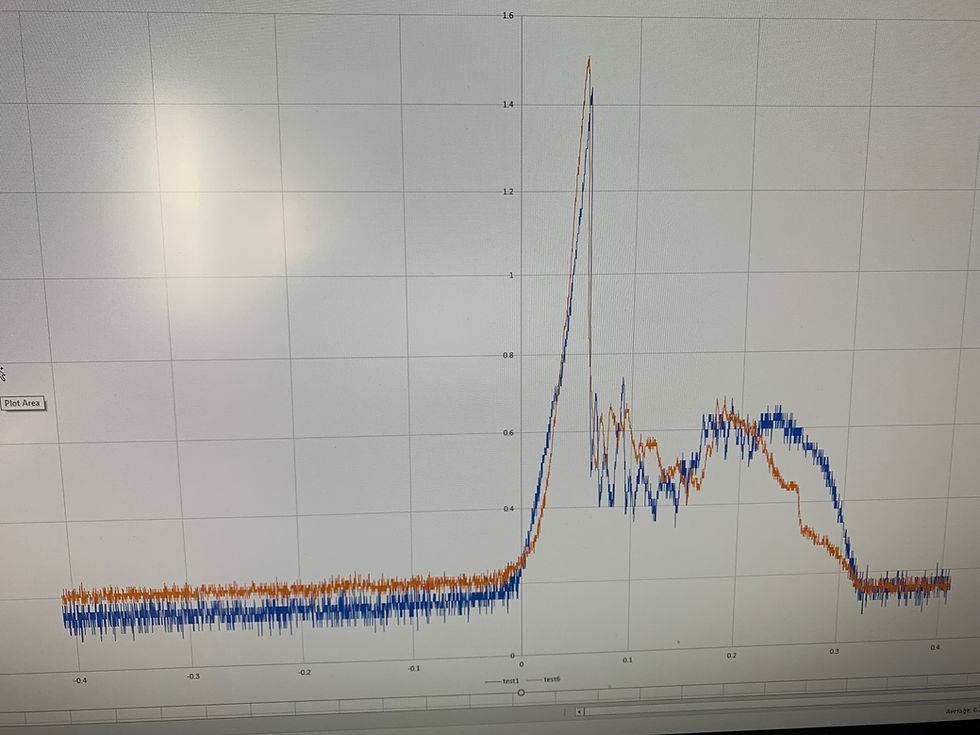
Even though I’m just turning things by hand I’m getting very nicely repeatable results. Ultimately I think I’ll need to turn the cube in a more precise way so that every turn is exactly the same. I’ll probably do this with some kind of servo motor. This way I’ll be able to compare the torque graphs for two different cubes turned at exactly the same rate.

Stay tuned for more updates soon!

Load cell: https://www.sparkfun.com/products/14727

Amplifier: http://www.ti.com/product/INA125

Oscilloscope: https://www.sparkfun.com/products/retired/10806

Cube Dimensions

In designing the Cube of Cubes we wanted to be able to store a reasonably wide variety of puzzles, but also make the Cube of Cubes itself look like a single coherent object once all the slots were filled. Basically, to make the Cube of Cubes look as cool as possible the gaps between the cubes have to be as small as possible, but smaller gaps mean larger cubes won’t fit.

To understand this problem better we created a graph of the sizes of common cubes. This data was taken from TheCubicle.us who kindly list the size of most of the cubes they sell.

There is a much greater range in cube sizes for 3x3s than other cube types. This is because there are more novelty 3x3 cubes than novelty cubes for any other size. 

But most cubers probably don’t have as many of these weird novelty cubes as they have cubes that are more typical of each cube type. So let’s try deleting the keychain cubes, treasure box cubes, and the giant oversized cubes. Then we get a much smaller range of cubes sizes to deal with. 

The smallest cube is the MoFang JiaoShi Mini 3x3 at 45 mm and the largest is the MF7 7x7 at 71 mm. So the maximum size difference is 26 mm, or about an inch.

We could now design a Cube of Cubes that could accommodate the largest cube size in any of the slots, but most people probably don’t have twenty-five 7x7s that they want to store. (I mean, look, I know some of you probably do have twenty-five 7x7s, and If you're one of these people email us. Not for any particular reason, I just want to know more about you.) 

But basically we think big gaps between puzzles makes the Cube of Cubes look worse because there is too much empty space. We assume that people’s cube collections will have more 3x3s than other puzzles, and probably more 2x2s - 5x5s than 6x6s and 7x7s. So instead of creating enough space to put a 7x7 anywhere we made the standard slot size smaller and you just have to put those larger puzzles in the four top corner spots.

While we’re looking at the cube data let’s just throw some really big cubes into the mix, but don’t go trying to store these in a Cube of Cubes! Here is the graph again with 8x8s, 9x9s, 10x10s, 11x11s, 13x13s, 15x15s, and 17x17s included: