In designing the Cube of Cubes we wanted to be able to store a reasonably wide variety of puzzles, but also make the Cube of Cubes itself look like a single coherent object once all the slots were filled. Basically, to make the Cube of Cubes look as cool as possible the gaps between the cubes have to be as small as possible, but smaller gaps mean larger cubes won’t fit.
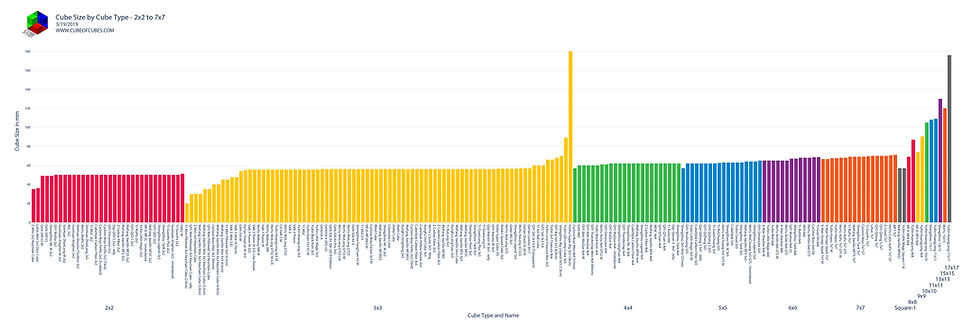
To understand this problem better we created a graph of the sizes of common cubes. This data was taken from TheCubicle.us who kindly list the size of most of the cubes they sell.
There is a much greater range in cube sizes for 3x3s than other cube types. This is because there are more novelty 3x3 cubes than novelty cubes for any other size.
But most cubers probably don’t have as many of these weird novelty cubes as they have cubes that are more typical of each cube type. So let’s try deleting the keychain cubes, treasure box cubes, and the giant oversized cubes. Then we get a much smaller range of cubes sizes to deal with.
The smallest cube is the MoFang JiaoShi Mini 3x3 at 45 mm and the largest is the MF7 7x7 at 71 mm. So the maximum size difference is 26 mm, or about an inch.
We could now design a Cube of Cubes that could accommodate the largest cube size in any of the slots, but most people probably don’t have twenty-five 7x7s that they want to store. (I mean, look, I know some of you probably do have twenty-five 7x7s, and If you're one of these people email us. Not for any particular reason, I just want to know more about you.)
But basically we think big gaps between puzzles makes the Cube of Cubes look worse because there is too much empty space. We assume that people’s cube collections will have more 3x3s than other puzzles, and probably more 2x2s - 5x5s than 6x6s and 7x7s. So instead of creating enough space to put a 7x7 anywhere we made the standard slot size smaller and you just have to put those larger puzzles in the four top corner spots.
While we’re looking at the cube data let’s just throw some really big cubes into the mix, but don’t go trying to store these in a Cube of Cubes! Here is the graph again with 8x8s, 9x9s, 10x10s, 11x11s, 13x13s, 15x15s, and 17x17s included:



Comments